
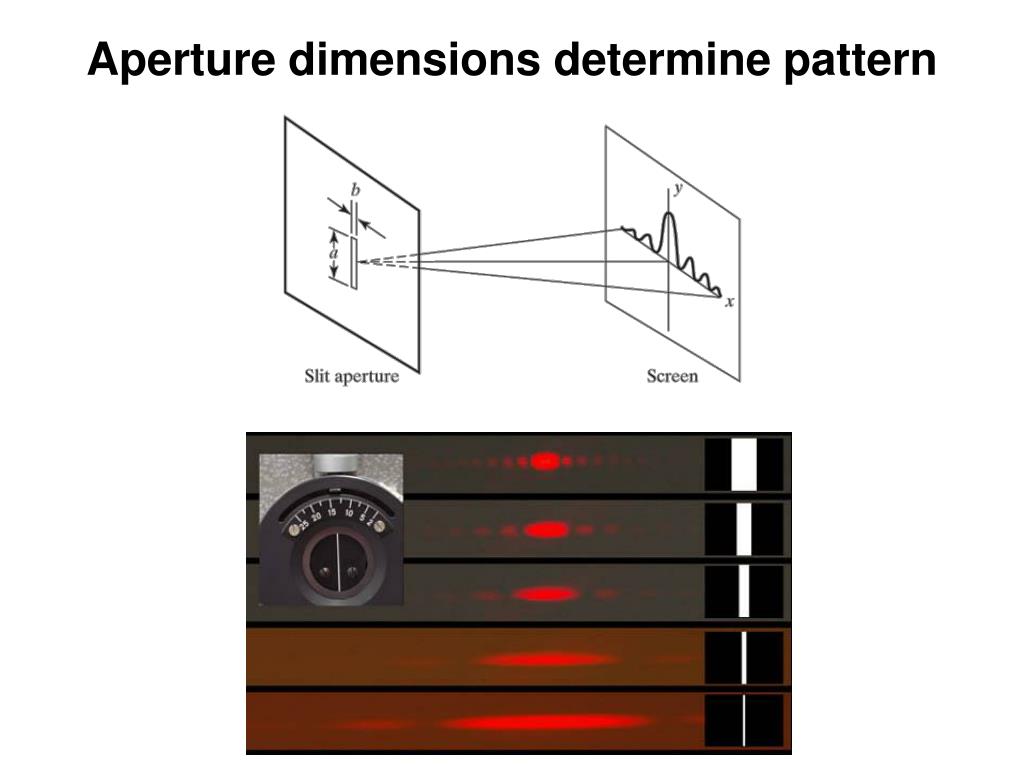
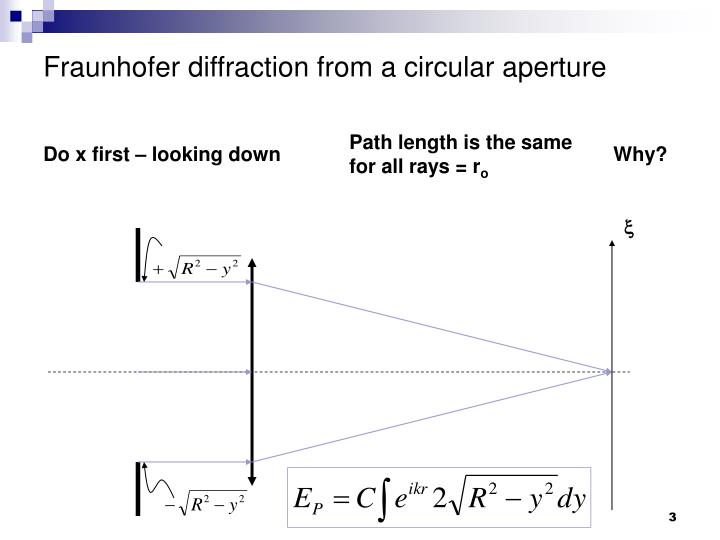
You can produce experimentally a Fraunhofer diffraction pattern.
FRAUNHOFER DIFFRACTION CIRCULAR APERTURE FULL
In the direction of the plane wave, the intensity is non-zero when one obstacle is finite and the other is infinite (as is the case here), the finite one (circular stop) yields full intensity, and the infinite one (hole) yields zero intensity: the energy passing through the hole is negligible as compared to that passing around the stop (we are in Fraunhofer conditions, at infinity, a finite energy gives infinitesimally small intensity).Ģ) The Poisson-Arago spot is a specific phenomenon observed in Fresnel regime.Ībout the Fraunhofer regime: it is not only a limiting case. This observation is the gist of Babinet's principle in Fraunhofer conditions: in any direction other than that of the incident plane wave, the intensity is zero, so the complementary obstacles yield the same pattern in those directions. In fact, they give the same intensity pattern when taken individually, because the only way to interfere destructively is to be in phase opposition (same absolute value of amplitude, but opposite signs). Two waves that would interfere destructively, give non-zero intensities when taken individually. Why? Because waves are made of amplitudes, but patterns are made of intensities, that is: squared amplitudes. I think you are missing things in both points.ġ) There is no reason why the sum of diffracted patterns would give a uniform intensity. So there is certainly no contradiction in this limit. the diffraction pattern in the Fraunhofer limit does not have a spot in the middle. I think the confusion might simply come from that the OP used an argument about the interference pattern in Fraunhofer diffraction and added the Arago spot into the mix, which does not actually appear there, i.e. We don't even need to consider the applicability of Babinet's principle though. Therefore I will only claim that this is a possible answer, which relies upon Babinet's principle only applying in the Fraunhofer limit. However I don't completely understand which limits Babinet's principle applies in. If I believe the OP, and also this article seems to assume the Fraunhofer limit, the contradiction is resolved. In other words, when the Fraunhofer criteria are met, complementary obstacles produce complementary diffraction patterns.

Anyone has input on this ?Īccording to wikipedia's article about the Poisson-Arago spot it is a phenomenon occurring in Fresnel diffraction, which is a different limit from Fraunhofer diffraction.

What am I missing ? I somehow have the feeling that patterns are complementary "everywhere except the center" because there is something ill-defined about using Huygens wavelets to predict the center of the pattern. Therefore these patterns are NOT complementary. In other words, when the Fraunhofer criteria are met, complementary obstacles produce complementary diffraction patterns.Ģ) Experiment shows that a circular stop and a circular aperture indeed produce opposite fringes, but the circular stop's diffraction pattern has the Poisson-Arago spot in the middle, while the circular aperture doesn't have a corresponding dark spot in the middle. In other words, the SUM of the diffracted patterns is expected to be a uniform intensity on the screen (all the wavelets = same as what we have when there is NO obstacle). My theoretical analysis leads to contradictory conclusions about such situations.ġ) Assuming incident light is a plane wave consisting of N sources of Huygens wavelets, obstacle 1 keeps a subset of those wavelets (blocking the others) while the obstacle 2 keeps the complementary subset of wavelets. For example, a circular aperture and a circular stop of same radii.


 0 kommentar(er)
0 kommentar(er)
